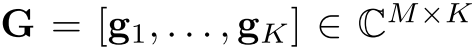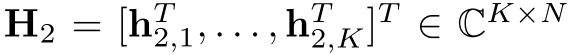论文精读笔记——Achievable Rate Maximization by Passive Intelligent Mirrors
Intro
多媒体通信课堂报告，选取ICASSP2018中的Achievable Rate Maximization by Passive Intelligent Mirrors一文。
ABSTRACT
使用Passive Intelligent Mirrors（PIM，无源智能反射镜）来操作多用户MISO下行链路通信。
设计transmit powers（传输功率）和mirror reflection coefficient（镜像反射系数）：保证移动用户的个人Quality of Service（QoS）需求的前提下，使sum-rate（和速率）最大化。
问题特点：non-convex（非凸）
solution：alternating maximization（交替极大化）与majorization-minimization算法（优化极小化算法）相结合。
merit：在不需要额外的能量消耗的情况下，system throughput（系统吞吐量）至少提高了40%。
1. INTRODUCTION
无线设备数量直奔500亿（50 billions）
对蜂窝网络的要求：
- 比现有网络高1000倍的数据速率
- 耗能减半
绿色节能的无线解决方案：
- renewable energy sources（可再生能源）
- energy-efficient hardware（节能硬件）
- green radio resource allocation and transmission（绿色无线电资源分配和传输）
具有巨大潜力的技术：Passive Intelligent Mirrors (PIM)——由许多small-unit reflector（小型单元反射镜）组成的physical metasurface（物理超表面），配备了simple low-cost sensors（简单的低成本传感器）和cognitive engine（认知引擎）。
metasurface（超表面）：指一种厚度小于波长的人工层状材料。超表面可实现对电磁波偏振、振幅、相位、极化方式、传播模式等特性的灵活有效调控。
对于任何一个入射electromagnetic field（电磁场），反射单元都能反射出phase-shifted（相移）的形式。因此通过设计适当的相移，可以组合不同单元反射的信号，使PIM成为一个active medium（激活媒质，工作媒质）。
PIM：充当一个amplify-and-forward relay（放大和转发中继），并不需要专用能源。作用：
- 节省宝贵的能源
- 在信道条件差的情况下也能进行通信
- 部署成本低
PIM使用范围：
- 集成到发射机周围建筑物的墙壁中
- 移动列车的天花板
- 笔记本电脑袋
- 人的手臂
- ……
intelligent wall（智能墙）：一种可以安装在建筑物内部以改善室内通信的墙。
related work：以往的工作并没有提供任何系统设计方法，只是将PIM的思想引入到室内场景中。
本文：主要针对室外场景，考虑一个MISO下行链路信道。工作：优化发射功率&PIM相移，目标：系统和速率最大化。
所得的优化问题：非凸问题
解决：结合交替优化和MM算法，提出可证明收敛、低复杂度的优化方法
结果：PIM可以在不增加任何能量消耗的情况下使系统的和速率提高40%以上
2. SYSTEM MODEL
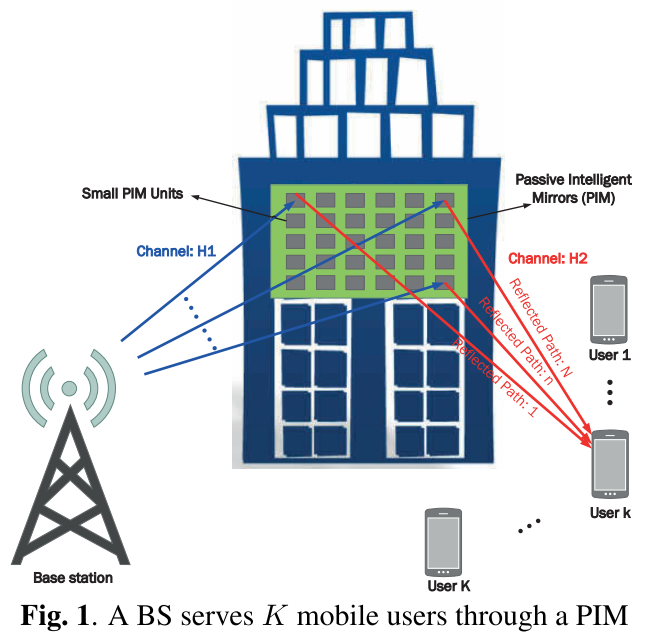
Figure 1：M根antennas（天线）的base station（BS，基站），通过嵌入周围建筑物中的N个反射单元组成的PIM（充当一个中继），为K个单天线用户（K个mobile）服务。
忽略BS和mobile的直接路径 ∵假设没有line-of-sight communication（直视通信线）
在用户k处接收到的离散时间信号可以写成（对于某个用户k来说）：
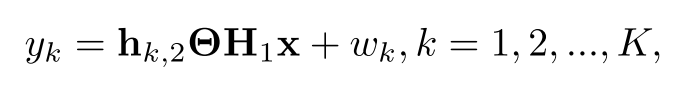
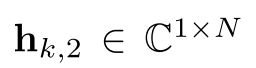：PIM和用户k之间的信道矩阵，1×N
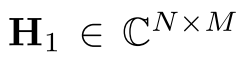：BS和PIM之间的信道，N×M
这两个是标准高斯变量（standard Gaussian variables），并且：
独立同分布（independent and identically distributed，i.i.d.）
复圆周对称（complex circularly symmetric）
独立同分布（independent and identically distributed，i.i.d.）：在概率统计理论中，指随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。
复圆周对称（circular symmetry）： its real and imaginary parts are independent and have the same distribution.
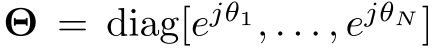：PIM相移矩阵，N×N
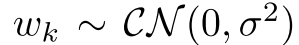：用户k的热噪声
thermal noise（热噪声）：
热噪声亦称白噪声，是由导体中电子的热震动引起的，它存在于所有电子器件和传输介质中。它是温度变化的结果，但不受频率变化的影响。热噪声是在所有频谱中以相同的形态分布，它是不能够消除的，由此对通信系统性能构成了上限。
- 由电阻等导体中自由电子的布朗运动引起的噪声；
- 电子的这种随机运动会产生一个交流电流成分，即热噪声；
- 频谱像白光的频谱在可见光的频谱范围内一样的均匀分布，又称白噪声。
- 服从高斯分布，又常称高斯白噪声。
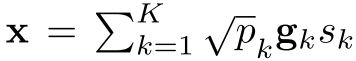：基站发射的信号，其中：
- p：发射功率（transmit power）
- g：信息符号（information symbol）（M×1矩阵）
- s：波束成形向量（beamforming vector）
对于用户k来说，SINR（信号与干扰加噪声比，Signal to Interference plus Noise Ratio）为：
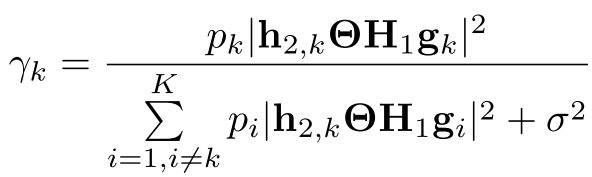
2.1 Problem formulation
工作目标：优化发射功率和矩阵Θ，以达到系统和速率的最大化
使问题易处理：采用zero-forcing transmission（迫零传输）——在高信噪比条件下最优
假设N≥K，定义：
迫零传输通过设置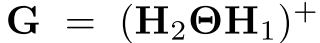
实现。
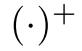代表伪逆矩阵（pseudo-inversion）
然后，
- 定义矩阵：
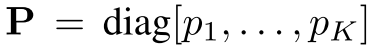
- 定义基站的最大可行发射功率：
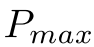
- 定义第k个用户的需求速率：
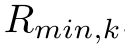
和速率最大化的问题可以如下表述：
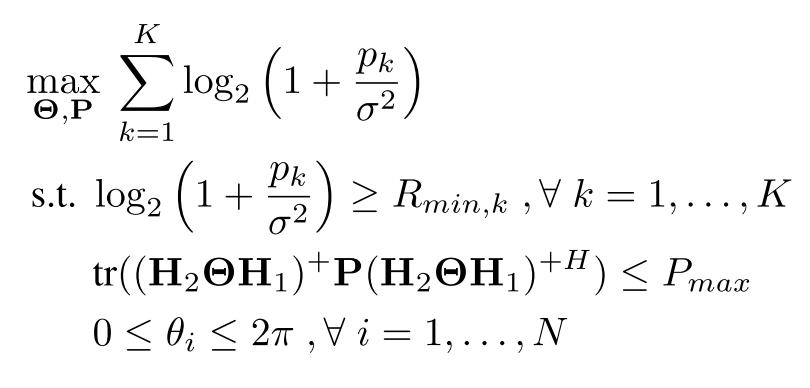
这是一个非凸问题，并且对于Θ的优化具有挑战性。Section3将介绍一种计算上可承受的（computationally-affordable）方法
3. PROPOSED APPROACH
解决计算复杂性：把P和Θ分别、迭代地优化。
3.1. Optimization with respect to Θ
对于固定的P，问题变成了一个可行性试验：
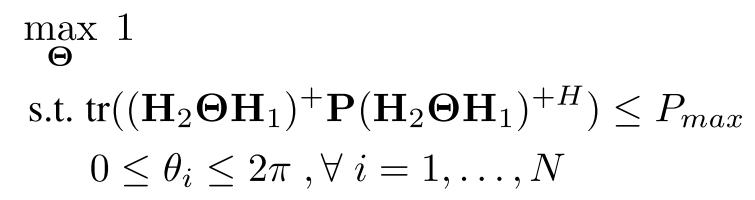
用一个变量替换：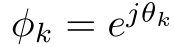
，问题变成了：
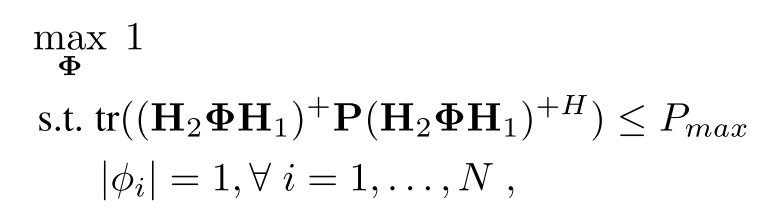
问题在于：目标函数不可微分，并且最后一个条件是非凸限制。
接着，作者观察到该问题是有解的，当且仅当：
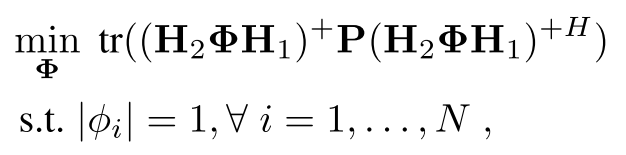这个问题里的目标函数的最小值小于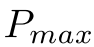。因此，目标函数可以再次改写为：
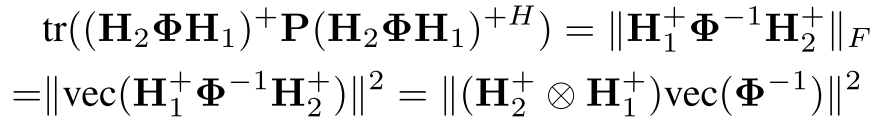
vec()：向量化算符，拉成列向量
⊗：张量积
||·||F：Frobenius 范数，简称F-范数，是一种矩阵范数，记为||·||F。矩阵A的Frobenius范数定义为矩阵A各项元素的绝对值平方的总和开根，可用于利用低秩矩阵来近似单一数据矩阵。用数学表示就是去找一个秩为k的矩阵B，使得矩阵B与原始数据矩阵A的差的F范数尽可能地小。
在这里，利用了Frobenius矩阵范数（Frobenius matrix norm）的性质&向量化算子（vectorization operator）与Kronecker积（克罗内克积，Kronecker product）之间的联系。这个新的目标函数可以处理非凸限制——前提是把它转化为可微函数。
使用：MM算法（Majorization-Minimization method），一个迭代方法，在第i次迭代时最大化目标函数的上限。
MM算法是一种迭代优化方法，它利用函数的凸性来找到它们的最大值或最小值。当目标函数f(θ)较难优化时，算法不直接对目标函数求最优化解，转而寻找一个易于优化的目标函数g(θ)替代，然后对这个替代函数求解，g(θ)的最优解逼近于f(θ)的最优解。每迭代一次，根据所求解构造用于下一次迭代的新的替代函数，然后对新的替代函数最优化求解得到下一次迭代的求解。通过多次迭代，可以得到越来越接近目标函数最优解的解。
Majorize-Minimization：每次迭代找到一个目标函数的上界函数，求上界函数的最小值。Majorization-Minimization的名字就是这么来的，找一个在上面的函数u——Majorization，最小化函数u——Minimization。
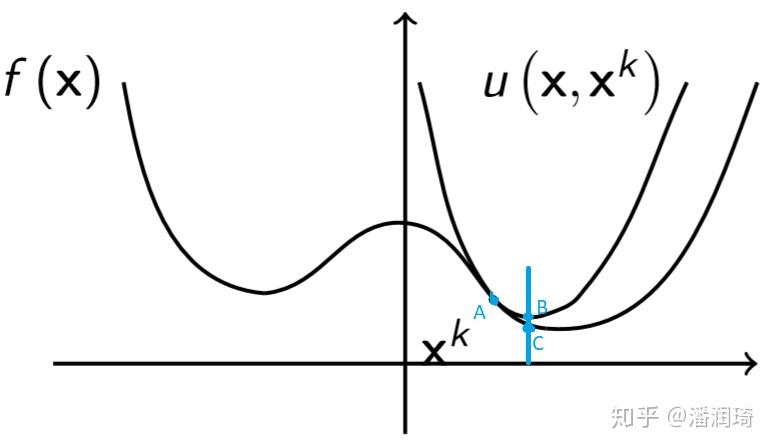
然而，对于任何第i次迭代，当在第(i−1)次迭代中计算的最大化值时，需要保证第i次迭代中最大化的上界和真实目标函数的上界必须相等。
MM算法的property（性质）：单调改进（monotonic improvement），即每次迭代后都单调地减少真正目标函数的值。——意味着最终会收敛于目标值 ∵目标函数在问题可行集上有下界。
使用MM算法的挑战：确定真实目标函数的合适上界，该上界需要：
- 满足MM算法的理论要求（即和真实目标函数的上界必须相等）
- 与原始目标函数相比更容易最小化
提出lemma（引理），给出一个方便确定的上界：
利用（8）式中的二阶泰勒展开式证明，在这里作者由于篇幅限制省略了证明的过程……
基于引理1，对于MM算法的每次迭代，面对的问题转化为：
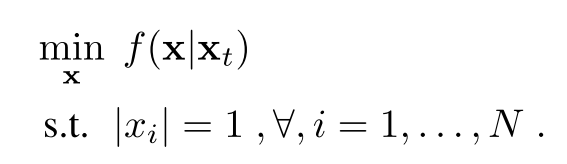
再提出命题：
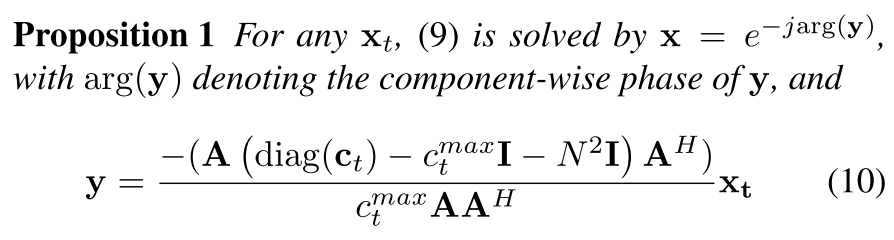
利用上面问题目标函数的驻点分析来证明，同样省略了证明过程。
3.2 Optimization with respect to P
对于固定的Θ，问题为：
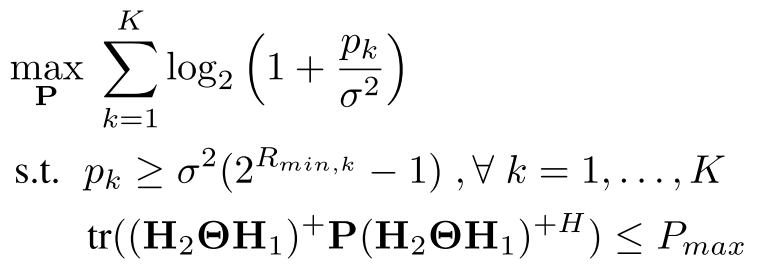
一个凸问题，可以直接用标准凸优化的方法。分析它的Karush–Kuhn–Tucker (KKT) optimality condi- tions（KKT最优化条件），引出该问题的闭式表达式（closed-form expression）的解：
Karush-Kuhn-Tucker (KKT)条件是非线性规划(nonlinear programming)最佳解的必要条件，将Lagrange乘数法(Lagrange multipliers)所处理涉及等式的约束优化问题推广至不等式。
闭式：一个表达式，由初等函数经过有限次的初等运算复合而成。
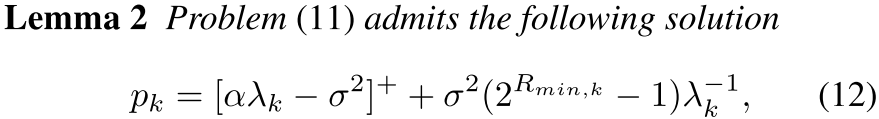
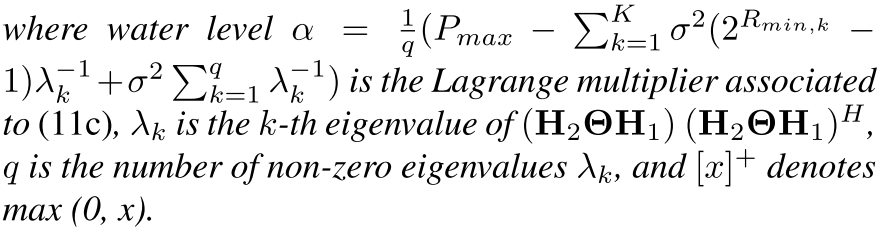
完整算法总结：
内循环：MM算法
外循环：交替最大化（alternating maximization）
算法的每次迭代使整个问题的目标函数（最开头未转化时的那个max值）值单调递增，最终收敛于目标函数值 ∵目标函数在紧可行域（闭集且有界）上是连续的，因此必有上界。
4. NUMERICAL RESULTS
做一个数值仿真，场景同第二章所述：
- 用户在625平方米的区域内被随机安排位置
- 信道为随机矩阵的实现，标准复高斯分布，独立同分布
所有结果通过平均了500多个独立信道和用户位置得到的
定义信噪比：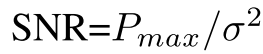
图2：SNR-可实现的和速率
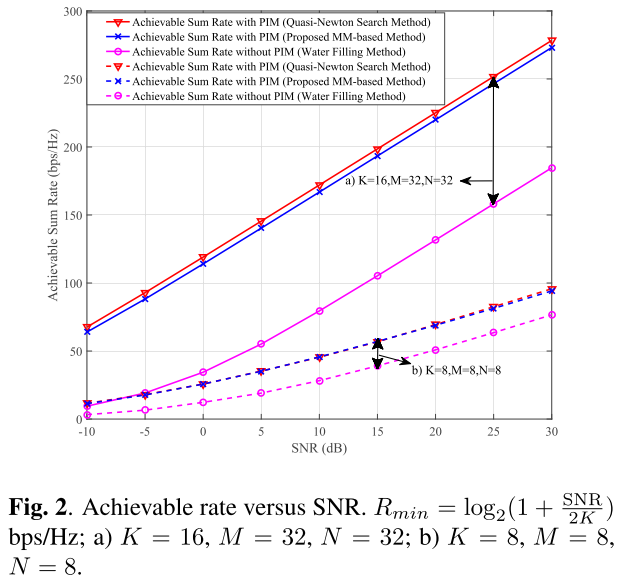
考虑了两组系统参数：
- K = 16, M = 32, N = 32
- K = 8, M = 8, N = 8
最小QoS速率设置为那个Rmin。
问题的最优解由拟牛顿法（共轭方向法，Quasi-Newton search）获得，算法复杂度是指数级别的，且只考虑benchmarking purpose（基准、标杆测试）。
在没有PIM的系统中：资源分配也被视为一个基线方案，这种情况下只需进行功率分配（就是3.2节Optimization with respect to P完成的工作）
由图可见，PIM提高了大于40%的和速率。随着天线和PIM单元的数量增加，差异变得更大。与更高复杂度的全局优化方法相比，PIM与其的差距始终有限。
图3：PIM单元数量-可实现的和频谱利用率
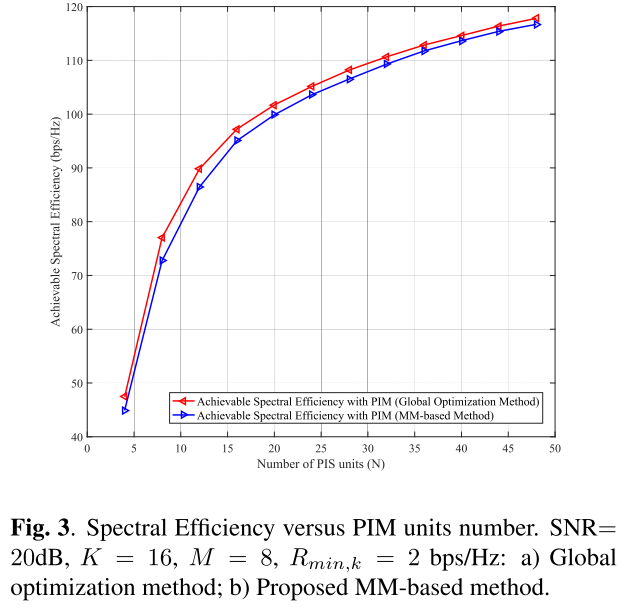
参数：SNR = 20 dB, K = 16, M = 8, Rmin,k = 2 bps/Hz
如图所示，PIM所提出的算法1与全局优化方法得到的结果十分接近。PIM单元越多，在一个蜂窝里的和频谱利用率越高，但PIM单元数目越来越多时会接近饱和。
图4：迭代次数-MSE
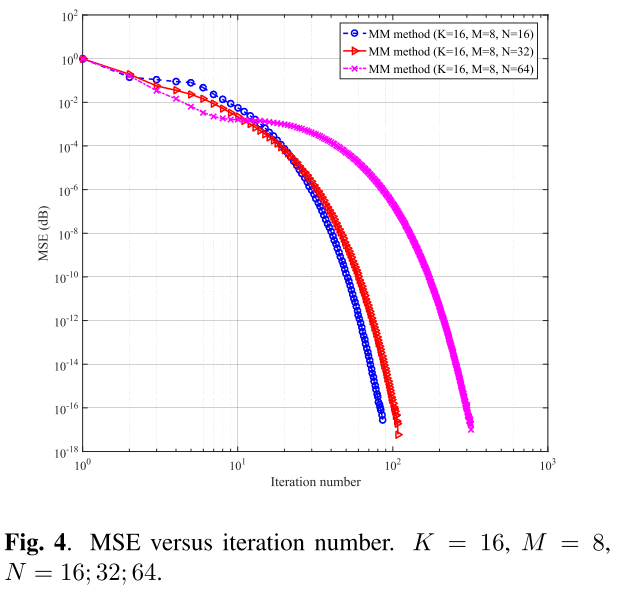
研究基于MM的算法1的收敛速度，基于该指标：达到给定的在两次连续迭代中的均方误差（Mean Square Error，MSE）所需要的迭代次数。MSE定义为：
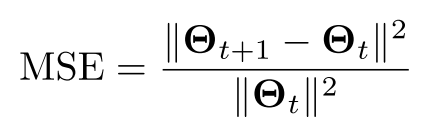
系统参数：K = 16, M = 8, N = 16; 32; 64
如图所示，MM算法在几十次迭代中即可达到可接受的MSE值。N越大，MSE值也越大——因为对应于待优化的变量的数量也在增加。
回顾MM算法的每个迭代只涉及简单的闭式计算，图4证实了所提出的基于MM的算法的非常有限的复杂性。
5. CONCLUSION
提出了一种基于PIM的多用户MIMO系统的和速率最大化方案。
将MM和交替优化相结合，解决了非凸无线资源分配问题，给出了一种可证明收敛且低复杂度的算法。
数值结果表明，该方案达到了近似最优的性能，与传统的无PIM系统相比，其和速率提高了40%以上。
